- T. Isernia, Bmo regularity for asymptotic parabolic systems with linear growth, Differential Integral Equations 28 (2015), no. 11-12, 1173–1196.
- T. Isernia, C. Leone & A. Verde, Partial regularity results for asymptotic quasi-convex functionals with general growth, Ann. Acad. Sci. Fenn. Math. 41 (2016), 817–844.
- V. Ambrosio & T. Isernia, A multiplicity result for a fractional Kirchhoff equation in
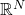 with a general nonlinearity, Commun. Contemp. Math. 20 (2018), no. 5, 1750054, 17 pp.
with a general nonlinearity, Commun. Contemp. Math. 20 (2018), no. 5, 1750054, 17 pp. - T. Isernia, Positive solution for nonhomogeneous sublinear fractional equations in
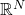 , Complex Var. Elliptic Equ. 63 (2018), no. 5, 689–714.
, Complex Var. Elliptic Equ. 63 (2018), no. 5, 689–714. - V. Ambrosio & T. Isernia, Concentration phenomena for a fractional Schrödinger–Kirchhoff type equation, Math. Methods Appl. Sci. 41 (2018), no. 2, 615–645.
- V. Ambrosio & T. Isernia, Sign-changing solutions for a class of Schrödinger equations with vanishing potentials, Rend. Lincei Mat. Appl. 29 (2018), 127–152.
- T. Isernia,
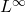 —regularity for a wide class of parabolic systems with general growth, Proc. Amer. Math. Soc. 146 (2018), no. 11, 4741–4753.
—regularity for a wide class of parabolic systems with general growth, Proc. Amer. Math. Soc. 146 (2018), no. 11, 4741–4753. - T. Isernia, Nonhomogeneous sublinear fractional Schrödinger equations, Two non-linear days in Urbino 2017. Electron. J. Diff. Eqns., Conf. 25 (2018), pp. 149–165.
- V. Ambrosio & T. Isernia, On a fractional
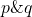 Laplacian problem with critical Sobolev-Hardy exponents, Mediterr. J. Math. 15 (2018), no. 6, 15:219.
Laplacian problem with critical Sobolev-Hardy exponents, Mediterr. J. Math. 15 (2018), no. 6, 15:219. - V. Ambrosio & T. Isernia, Multiplicity and concentration results for some nonlinear Schrödinger equations with the fractional
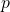 –Laplacian, Discrete Contin. Dyn. Syst. 38 (2018), no.11, 5835–5881.
–Laplacian, Discrete Contin. Dyn. Syst. 38 (2018), no.11, 5835–5881. - V. Ambrosio, T. Isernia & G. Siciliano, On a fractional
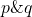 Laplacian problem with critical growth, Minimax Theory Appl. 4 (2019), no.1, 1-9.
Laplacian problem with critical growth, Minimax Theory Appl. 4 (2019), no.1, 1-9. - V. Ambrosio, G. Figueiredo, T. Isernia & G. Molica Bisci, Sign-changing solutions for a class of zero mass nonlocal Schrödinger equations, Adv. Nonlinear Stud. 19 (2019), no. 1, 113–132.
- V. Ambrosio & T. Isernia, On the multiplicity and concentration for
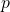 -fractional Schrödinger equations, Appl. Math. Lett. 95 (2019), 13-22.
-fractional Schrödinger equations, Appl. Math. Lett. 95 (2019), 13-22. - C.O. Alves, V. Ambrosio & T. Isernia, Existence, multiplicity and concentration for a class of fractional
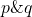 Laplacian problems in
Laplacian problems in 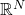 , Comm. Pura App. Anal. 18 (2019), no. 4, 2009–2045.
, Comm. Pura App. Anal. 18 (2019), no. 4, 2009–2045. - V. Ambrosio, A. Fiscella & T. Isernia, Infinitely many solutions for fractional Kirchhoff-Sobolev-Hardy critical problems, Electron. J. Qual. Theory Differ. Equ. 2019, No. 25, 1-13.
- T. Isernia, On a nonhomogeneous sublinear-superlinear fractional equation in
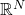 , Riv. Math. Univ. Parma (N.S.) 10 (2019), no.1, 167-186.
, Riv. Math. Univ. Parma (N.S.) 10 (2019), no.1, 167-186. - V. Ambrosio, G.M. Figueiredo & T. Isernia, Existence and concentration of positive solutions for
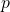 -fractional Schrödinger equations, accepted for publication on Ann. Mat. Pura Appl.
-fractional Schrödinger equations, accepted for publication on Ann. Mat. Pura Appl. - S. Biagi & T. Isernia, On the solvability of singular boundary value problems on the real line in the critical growth case, accepted for publication on Discrete Contin. Dyn. Syst.
- T. Isernia, Sign-changing solutions for a fractional Kirchhoff equation, accepted for publication on Nonlinear Analysis.
- T. Isernia, Fractional
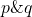 -Laplacian problems with potentials vanishing at infinity, Opuscula Math. 40, no. 1 (2020), 93–110.
-Laplacian problems with potentials vanishing at infinity, Opuscula Math. 40, no. 1 (2020), 93–110. - V. Ambrosio, T. Isernia & V. Radulescu, Concentration of positive solutions for a class of fractional
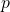 -Kirchhoff type equations, Proc. Roy. Soc. Edinburgh Sect. A 151 (2021), no. 2, 601–651.
-Kirchhoff type equations, Proc. Roy. Soc. Edinburgh Sect. A 151 (2021), no. 2, 601–651. - V. Ambrosio & T. Isernia, Multiplicity of positive solutions for a fractional
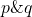 -Laplacian problem in
-Laplacian problem in 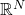 , J. Math. Anal. Appl. 501 (2021), no. 1, 124487, 31 pp.
, J. Math. Anal. Appl. 501 (2021), no. 1, 124487, 31 pp. - T. Isernia & D. Repovs, Nodal solutions for double phase Kirchhoff problems with vanishing potentials, Asymptotic Analysis 1 (2020), 1–26.
- V. Ambrosio & T. Isernia, A multiplicity result for a
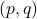 -Schrödinger-Kirchhoff type equation, Ann. Mat. Pura Appl. (4) 201 (2022), no. 2, 943–984.
-Schrödinger-Kirchhoff type equation, Ann. Mat. Pura Appl. (4) 201 (2022), no. 2, 943–984. - T. Isernia, C. Leone & A. Verde, Partial regularity result for non-autonomous elliptic systems with general growth, Commun. Pure Appl. Anal. 20 (2021), no. 12, 4271–4305.
- T. Isernia, C. Leone & A. Verde, Partial Regularity for elliptic systems with critical growth, Atti Accad. Naz. Lincei Rend. Lincei Mat. Appl. 33 (2022), no. 2, 271–296.
- V. Ambrosio & T. Isernia, The critical fractional Ambrosetti-Prodi problem, Rend. Circ. Mat. Palermo (2) 71 (2022), no. 3, 1107–1132.
- M. Foss, T. Isernia, C. Leone & A. Verde, A-caloric approximation and partial regularity for parabolic systems with Orlicz growth, Calc. Var. Partial Differential Equations 62 (2023), no. 2, Paper No. 51, 39 pp.
- F. Anceschi & T. Isernia,
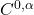 partial regularity result for elliptic systems with discontinuous coefficients and Orlicz growth, J. Math. Anal. Appl. 530 (2024), no.1, Paper No.127628.
partial regularity result for elliptic systems with discontinuous coefficients and Orlicz growth, J. Math. Anal. Appl. 530 (2024), no.1, Paper No.127628. - V. Ambrosio & T. Isernia, Ground state solutions for a
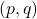 -Choquard equation with a general nonlinearity, J. Differential Equations 401 (2024), 428-468.
-Choquard equation with a general nonlinearity, J. Differential Equations 401 (2024), 428-468. - V. Ambrosio, G. Autuori & T. Isernia, Ground state solutions for a quasilinear Choquard equation with a general nonlinearity, Commun. Pure Appl. Anal. 23 (2024), no. 11, 1661-1678.
- A. Gentile, T. Isernia & A. Passarelli di Napoli, On a class of obstacle problems with
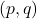 -growth and explicit
-growth and explicit 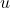 -dependence, Adv. Calc. Var. 18 (2025), no. 3, 943–962.
-dependence, Adv. Calc. Var. 18 (2025), no. 3, 943–962. - T. Isernia, On a critical superlinear fractional
 -Kirchhoff equation, J. Math. Anal. Appl. 550 (2025), no. 2, Paper No. 129626, 22 pp.
-Kirchhoff equation, J. Math. Anal. Appl. 550 (2025), no. 2, Paper No. 129626, 22 pp. - V. Ambrosio, T. Isernia & L. Temperini, Existence of ground state solutions for fractional Kirchhoff–Choquard equations, Discrete Contin. Dyn. Syst. 45 (12) (2025), pp. 4817–4851